Под рекурсивной функцией в программирование понимают функцию, которая вызывает сама себя. Рекурсивные функции чаще всего используют для компактной реализации рекурсивных алгоритмов. Классическими рекурсивными алгоритмами могут быть возведение числа в целую положительную степень, вычисление факториала.
Перейдет к примеру применения рекурсивной функции.
Задача:
Вычислить факториал числа n.
Для справки: «Факториалом числа N называют произведение всех натуральных чисел от 1 до N»
#include "stdafx.h"
#include <iostream>
using namespace std;
long int factorial(int n)
{
if (n<=1)
return (n);
else return(n*factorial(n-1));
}
int main ()
{
int i; long int f;
cout<<"i=";
cin>>i;
f=factorial(i);
cout<<i<<"!="<<f<<endl;
system("pause");
return 0;
}
Перегрузка функций
Язык C++ позволяет связать с одним и тем же именем функции различные определения, то есть возможно существование нескольких функций с одинаковым именем. У них может быть разное количество параметров или разные типы параметров. Эта возможность называется перегрузкой имени функции. Перегруженные функции создают, когда одно и то же действие следует выполнить над разными типами входных данных.
В приведенном далее тексте программы три функции с именем Pow. Первая выполняет операцию возведения вещественного числа a в дробную степень n=k/m, где k и m — целые числа. Вторая возводит вещественное число a в целую степень n, а третья — целое число a в целую степень n1. Какую именно функцию вызвать, компилятор определяет по типу фактических параметров.
Так, если a — вещественное число, а k — целое, то оператор Pow (a, k) вызовет вторую функцию, так как она имеет заголовок float Pow(float a, int n). Команда Pow((int) a, k) приведет к вызову третьей функции int Pow(int a, int n), так как вещественная переменная a преобразована к целому типу. Первая функция float Pow(float a, int k, int m) имеет три параметра, значит, обращение к ней осуществляется командой Pow (a, k, m).
#include "stdafx.h"
#include <iostream>
using namespace std;
//первая функция
float Pow(float a, int k, int m)
{
cout<<"function 1 \t";
if (a==0) return (0);
else if (k==0) return (1);
else if (a>0) return (exp((float)k/m*log(a)));
else if (m%2!=0) return (-(exp((float)k/m*log(-a))));
}
//вторая функция
float Pow(float a, int n)
{
if (a==0) {cout<<"function 2 \t"; return (0);}
else if (n==0) {cout<<"function 2 \t"; return (1);}
else if (n<0) return (1/Pow(a,-n));
else return (a*Pow(a,n-1));
}
//третья функция
int Pow(int a, int n)
{
if (a==0) {cout<<"function 3 \t"; return (0);}
else if (n==0) {cout<<"function 3 \t"; return (1);}
else if (n<0) return (1/Pow(a,-n));
else return (a*Pow(a,n-1));
}
int main ()
{
float a; int k, n, m;
cout<<"a="; cin>>a;
cout<<"k="; cin>>k;
cout<<"s="<<Pow(a, k)<<"\n"; //вызов второй функци
cout<<"s="<<Pow((int) a, k)<<"\n"; //вызов третьей функции
cout<<"a="; cin>>a;
cout<<"k="; cin>>k;
cout<<"m="; cin>>m;
cout<<"s="<<Pow(a, k, m)<<"\n"; //вызов первой функции
system("pause");
return 0;
}
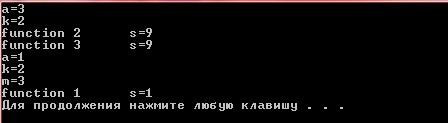
Результат работы программы:
На ранних этапах программирования вам скорее всего не понадобится перегрузка функций, но в будущем данная процедура может оказаться очень полезной для реализации специфического алгоритма.