Перед тем как начать изучение непосредственно алгоритмов, необходимо обладать базовыми знаниями касательно самих графов, понимать, как они представляются в компьютере. Здесь не будут подробно описаны все аспекты теории графов (этого и не требуется), но только те, незнание которых заметно усложнит усвоение данной области программирования.
Несколько примеров дадут немного поверхностного представления о графе. Так типичным графом является схема метро или какой-либо другой маршрут. В частности программисту знакома компьютерная сеть, также являющаяся графом. Общее здесь это наличие точек, соединенных линиями. Так в компьютерной сети точки – это отдельные серверы, а линии – различные виды электрических сигналов. В метрополитене первое – станции, второе – туннели, проложенные между ними. В теории графов точки именуется вершинами (узлами), а линии – ребрами (дугами). Таким образом, граф – это совокупность вершин, соединённых ребрами.
Математика оперирует не содержанием вещей, а их структурой, абстрагируя ее из всего того, что дано как целое. Пользуясь именно этим приемом, мы можем заключать о каких-либо объектах как о графах. А поскольку теория графов это часть математики, то для нее нет абсолютно никакого значения, что в принципе представляет собой объект; важно лишь то, является ли он графом, т. е. обладает ли обязательными для графов свойствами. Поэтому, прежде чем привести примеры, мы выделяем в рассматриваемом объекте лишь то, что как нам кажется, позволит показать аналогию, отыскиваем общее.
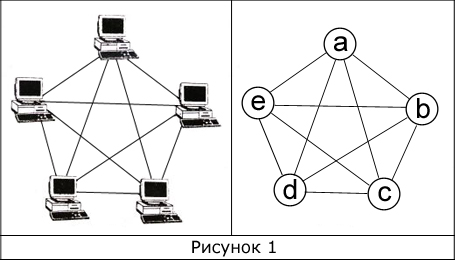
Вернемся к компьютерной сети. Она обладает определенной топологией, и может быть условно изображена в виде некоторого числа компьютеров и путей их соединяющих. На рисунке ниже в качестве примера показана полносвязная топология.
Это по сути граф. Пять компьютеров являются вершинами, а соединения (пути передачи сигналов) между ними – ребрами. Заменив компьютеры вершинами, мы получим математический объект – граф, который имеет 10 ребер и 5 вершин. Пронумеровать вершины можно произвольным образом, а не обязательно так, как это сделано на рисунке. Стоит отметить, что в данном примере не используется ни одной петли, то есть такого ребра, которое выходит из вершины и сразу же входит в нее, но петли могут встречаться в задачах.
Вот некоторые важные обозначения, используемые в теории графов:
- G=(V, E), здесь G – граф, V – его вершины, а E – ребра;
- |V| – порядок (число вершин);
- |E| – размер графа (число рёбер).
В нашем случае (рис. 1) |V|=5, |E|=10;
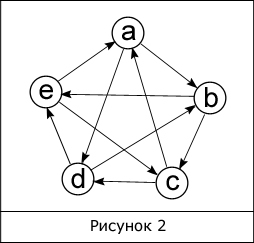
Когда из любой вершины доступна любая другая вершина, то такой граф называется неориентированным связным графом (рис. 1). Если же граф связный, но это условие не выполняется, тогда такой граф называется ориентированным или орграфом (рис. 2).
В ориентированных и неориентированных графах имеется понятие степени вершины. Степень вершины – это количество ребер, соединяющих ее с другими вершинами. Сумма всех степеней графа равна удвоенному количеству всех его ребер. Для рисунка 2 сумма всех степеней равна 20.
В орграфе, в отличие от неориентированного графа, имеется возможность двигаться из вершины h в вершину s без промежуточных вершин, лишь тогда когда ребро выходит из h и входит в s, но не наоборот.
Ориентированные графы имеют следующую форму записи:
G=(V, A), где V – вершины, A – направленные ребра.
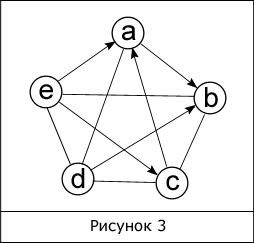
Третий тип графов – смешанные графы (рис. 3). Они имеют как направленные ребра, так и ненаправленные. Формально смешанный граф записывается так: G=(V, E, A), где каждая из букв в скобках обозначает тоже, что ей приписывалось ранее.
В графе на рисунке 3 одни дуги направленные [(e, a), (e, c), (a, b), (c, a), (d, b)], другие – ненаправленные [(e, d), (e, b), (d, c)…].
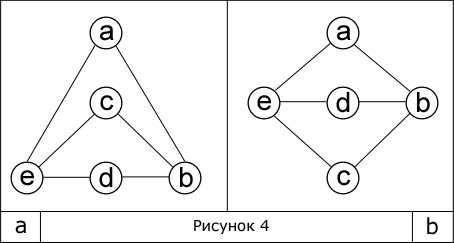
Два или более графов на первый взгляд могут показаться разными по своей структуре, что возникает вследствие различного их изображения. Но это не всегда так. Возьмем два графа (рис. 4).
Они эквивалентны друг другу, ведь не изменяя структуру одного графа можно построить другой. Такие графы называются изоморфными, т. е. обладающими тем свойством, что какая-либо вершина с определенным числом ребер в одном графе имеет тождественную вершину в другом. На рисунке 4 изображены два изоморфных графа.
Когда каждому ребру графа поставлено в соответствие некоторое значение, называемое весом ребра, тогда такой граф взвешенный. В разных задачах в качестве веса могут выступать различные виды измерений, например длины, цены маршруты и т. п. В графическом представлении графа весовые значения указываются, как правило, рядом с ребрами.
В любом из рассмотренных нами графов имеется возможность выделить путь и, причем не один. Путь – это последовательность вершин, каждая из которых соединена с последующей посредством ребра. Если первая и последняя вершины совпадают, то такой путь называется циклом. Длина пути определяется количеством составляющих его ребер. Например, на рисунке 4.а путем служит последовательность [(e), (a), (b), (c)]. Этот путь является подграфом, так как к нему применимо определение последнего, а именно: граф G’=(V’, E’) является подграфом графа G=(V, E), только тогда когда V’ и E’ принадлежат V, E.
Способы представления графов.
Граф, как и большинство других математических объектов, может быть представлен на компьютере (сохранен в его памяти). Существуют несколько способов его интерпретации, вот наиболее известные из них:
Использование двух первых методов предполагает хранение графа в виде двумерного массива (матрицы). Причем размеры этих массивов, зависят от количества вершин и/или ребер в конкретном графе. Так размер матрицы смежности n×n, где n – число вершин, а матрицы инцидентности n×m, n – число вершин, m – число ребер в графе.