Алгоритм голландского ученого Эдсгера Дейкстры находит все кратчайшие пути из одной изначально заданной вершины графа до всех остальных. С его помощью, при наличии всей необходимой информации, можно, например, узнать какую последовательность дорог лучше использовать, чтобы добраться из одного города до каждого из многих других, или в какие страны выгодней экспортировать нефть и тому подобное.
Минусом данного метода является невозможность обработки графов, в которых имеются ребра с отрицательным весом, т. е. если, например, некоторая система предусматривает убыточные для Вашей фирмы маршруты, то для работы с ней следует воспользоваться отличным от алгоритма Дейкстры методом.
Для программной реализации алгоритма понадобиться два массива: логический visited – для хранения информации о посещенных вершинах и численный distance, в который будут заноситься найденные кратчайшие пути. Итак, имеется граф G=(V, E). Каждая из вершин входящих во множество V, изначально отмечена как не посещенная, т. е. элементам массива visited присвоено значение false.
Поскольку самые выгодные пути только предстоит найти, в каждый элемент вектора distance записывается такое число, которое заведомо больше любого потенциального пути (обычно это число называют бесконечностью, но в программе используют, например максимальное значение конкретного типа данных). В качестве исходного пункта выбирается вершина s и ей приписывается нулевой путь: distance[s]=0, т. к. нет ребра из s в s (метод не предусматривает петель).
Далее, находятся все соседние вершины (в которые есть ребро из s) [пусть таковыми будут t и u] и поочередно исследуются, а именно вычисляется стоимость маршрута из s поочередно в каждую из них:
- distance[t]=distance[s]+весинцидентного s и t ребра;
- distance[u]=distance[s]+ весинцидентного s и u ребра.
Но вполне вероятно, что в ту или иную вершину из s существует несколько путей, поэтому цену пути в такую вершину в массиве distance придется пересматривать, тогда наибольшее (неоптимальное) значение игнорируется, а наименьшее ставиться в соответствие вершине.
После обработки смежных с s вершин она помечается как посещенная: visited[s]=true, и активной становится та вершина, путь из s в которую минимален. Допустим, путь из s в u короче, чем из s в t, следовательно, вершина u становиться активной и выше описанным образом исследуются ее соседи, за исключением вершины s. Далее, u помечается как пройденная: visited[u]=true, активной становится вершина t, и вся процедура повторяется для нее. Алгоритм Дейкстры продолжается до тех пор, пока все доступные из s вершины не будут исследованы.
Теперь на конкретном графе проследим работу алгоритма, найдем все кратчайшие пути между истоковой и всеми остальными вершинами. Размер (количество ребер) изображенного ниже графа равен 7 (|E|=7), а порядок (количество вершин) – 6 (|V|=6). Это взвешенный граф, каждому из его ребер поставлено в соответствие некоторое числовое значение, поэтому ценность маршрута необязательно определяется числом ребер, лежащих между парой вершин.

Из всех вершин входящих во множество V выберем одну, ту, от которой необходимо найти кратчайшие пути до остальных доступных вершин. Пусть таковой будет вершина 1. Длина пути до всех вершин, кроме первой, изначально равна бесконечности, а до нее – 0, т. к. граф не имеет петель.
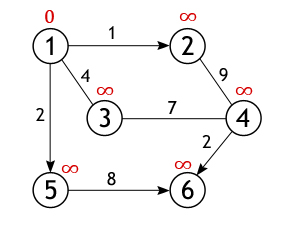
У вершины 1 ровно 3 соседа (вершины 2, 3, 5), и чтобы вычислить длину пути до них нужно сложить вес дуг, лежащих между вершинами: 1 и 2, 1 и 3, 1 и 5 со значением первой вершины (с нулем):
3←4+0
5←2+0
Как уже отмечалось, получившиеся значения присваиваются вершинам, лишь в том случае если они «лучше» (меньше) тех которые значатся на настоящий момент. А так как каждое из трех чисел меньше бесконечности, они становятся новыми величинами, определяющими длину пути из вершины 1 до вершин 2, 3 и 5.
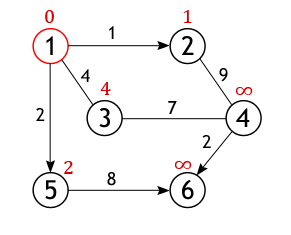
Далее, активная вершина помечается как посещенная, статус «активной» (красный круг) переходит к одной из ее соседок, а именно к вершине 2, поскольку она ближайшая к ранее активной вершине.

У вершины 2 всего один не рассмотренный сосед (вершина 1 помечена как посещенная), расстояние до которого из нее равно 9, но нам необходимо вычислить длину пути из истоковой вершины, для чего нужно сложить величину приписанную вершине 2 с весом дуги из нее в вершину 4
Условие «краткости» (10<∞) выполняется, следовательно, вершина 4 получает новое значение длины пути.
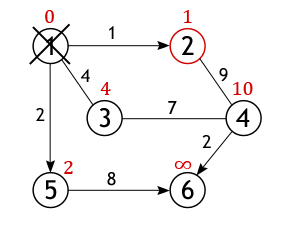
Вершина 2 перестает быть активной, также как и вершина 1 удаляется из списка не посещённых. Теперь тем же способом исследуются соседи вершины 5, и вычисляется расстояние до них.
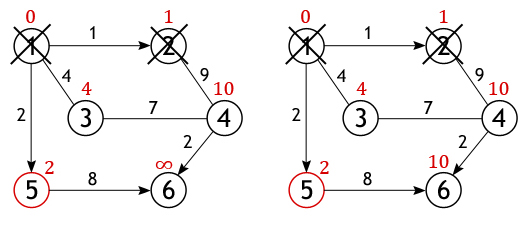
Когда дело доходит до осмотра соседей вершины 3, то тут важно не ошибиться, т. к. вершина 4 уже была исследована и расстояние одного из возможных путей из истока до нее вычислено. Если двигаться в нее через вершину 3, то путь составит 4+7=11, а 11>10, поэтому новое значение игнорируется, старое остается.

Аналогичная ситуация с вершиной 6. Значение самого близкого пути до нее из вершины 1 равно 10, а оно получается только в том случае, если идти через вершину 5.
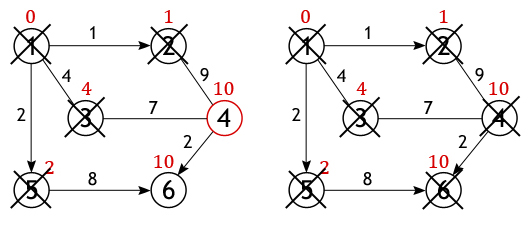
Когда все вершины графа, либо все те, что доступны из истока, будут помечены как посещенные, тогда работа алгоритма Дейкстры завершится, и все найденные пути будут кратчайшими. Так, например, будет выглядеть список самых оптимальных расстояний лежащих между вершиной 1 и всеми остальными вершинами, рассматриваемого графа:
1→2=1
1→3=4
1→4=10
1→5=2
1→6=10
В программе, находящей ближайшие пути между вершинами посредством метода Дейкстры, граф будет представлен в виде не бинарной матрицы смежности. Вместо единиц в ней будут выставлены веса ребер, функция нулей останется прежней: показывать, между какими вершинами нет ребер или же они есть, но отрицательно направленны.
Код программы на C++:
#include "stdafx.h"
#include <iostream>
using namespace std;
const int V=6;
//алгоритм Дейкстры
void Dijkstra(int GR[V][V], int st)
{
int distance[V], count, index, i, u, m=st+1;
bool visited[V];
for (i=0; i<V; i++)
{
distance[i]=INT_MAX; visited[i]=false;
}
distance[st]=0;
for (count=0; count<V-1; count++)
{
int min=INT_MAX;
for (i=0; i<V; i++)
if (!visited[i] && distance[i]<=min)
{
min=distance[i]; index=i;
}
u=index;
visited[u]=true;
for (i=0; i<V; i++)
if (!visited[i] && GR[u][i] && distance[u]!=INT_MAX &&
distance[u]+GR[u][i]<distance[i])
distance[i]=distance[u]+GR[u][i];
}
cout<<"Стоимость пути из начальной вершины до остальных:\t\n";
for (i=0; i<V; i++) if (distance[i]!=INT_MAX)
cout<<m<<" > "<<i+1<<" = "<<distance[i]<<endl;
else cout<<m<<" > "<<i+1<<" = "<<"маршрут недоступен"<<endl;
}
//главная функция
void main()
{
setlocale(LC_ALL, "Rus");
int start, GR[V][V]={
{0, 1, 4, 0, 2, 0},
{0, 0, 0, 9, 0, 0},
{4, 0, 0, 7, 0, 0},
{0, 9, 7, 0, 0, 2},
{0, 0, 0, 0, 0, 8},
{0, 0, 0, 0, 0, 0}};
cout<<"Начальная вершина >> "; cin>>start;
Dijkstra(GR, start-1);
system("pause>>void");
}
Код программы на Pascal:
program DijkstraAlgorithm;
uses crt;
const V=6; inf=100000;
type vektor=array[1..V] of integer;
var start: integer;
const GR: array[1..V, 1..V] of integer=(
(0, 1, 4, 0, 2, 0),
(0, 0, 0, 9, 0, 0),
(4, 0, 0, 7, 0, 0),
(0, 9, 7, 0, 0, 2),
(0, 0, 0, 0, 0, 8),
(0, 0, 0, 0, 0, 0));
{алгоритм Дейкстры}
procedure Dijkstra(GR: array[1..V, 1..V] of integer; st: integer);
var count, index, i, u, m, min: integer;
distance: vektor;
visited: array[1..V] of boolean;
begin
m:=st;
for i:=1 to V do
begin
distance[i]:=inf; visited[i]:=false;
end;
distance[st]:=0;
for count:=1 to V-1 do
begin
min:=inf;
for i:=1 to V do
if (not visited[i]) and (distance[i]<=min) then
begin
min:=distance[i]; index:=i;
end;
u:=index;
visited[u]:=true;
for i:=1 to V do
if (not visited[i]) and (GR[u, i]<>0) and (distance[u]<>inf) and
(distance[u]+GR[u, i]<distance[i]) then
distance[i]:=distance[u]+GR[u, i];
end;
write('Стоимость пути из начальной вершины до остальных:'); writeln;
for i:=1 to V do
if distance[i]<>inf then
writeln(m,' > ', i,' = ', distance[i])
else writeln(m,' > ', i,' = ', 'маршрут недоступен');
end;
{основной блок программы}
begin
clrscr;
write('Начальная вершина >> '); read(start);
Dijkstra(GR, start);
end.