Говорить о том, что ребро g и каждая из вершин u и y инцидентна g, стоит лишь в том случае, если g соединяет u и y. Уяснив это, перейдем к рассмотрению данного метода. Матрица инцидентности строиться по похожему, но не по тому же принципу, что и матрица смежности. Так если последняя имеет размер n×n, где n – число вершин, то матрица инцидентности – n×m, здесь n – число вершин графа, m – число ребер. То есть теперь чтобы задать значение какой-либо ячейки, нужно сопоставить не вершину с вершиной, а вершину с ребром.
В каждой ячейки матрицы инцидентности неориентированного графа стоит 0 или 1, а в случае ориентированного графа, вносятся 1, 0 или -1. То же самое, но наиболее структурировано:
1) Неориентированный граф
a. 1 – вершина инцидентна ребру
b. 0 – вершина не инцидентна ребру
2) Ориентированный граф
a. 1 – вершина инцидентна ребру, и является его началом
b. 0 – вершина не инцидентна ребру
c. -1 – вершина инцидентна ребру, и является его концом
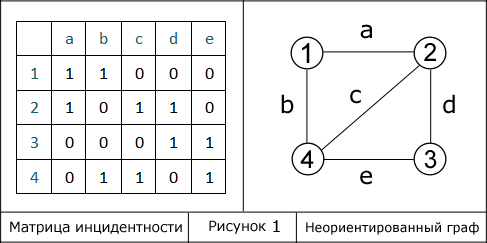
Построим матрицу инцидентности сначала для неориентированного графа, а затем для орграфа.
Ребра обозначены буквами от a до e, вершины – цифрами. Все ребра графа не направленны, поэтому матрица инцидентности заполнена положительными значениями.
Для орграфа графа матрица имеет немного другой вид. В каждую из ее ячеек внесено одно из трех значений. Обратите внимание, что нули в двух этих матрицах (рис. 1 и 2) занимают одинаковые позиции, ведь в обоих случаях структура графа одна. Но некоторые положительные единицы сменились на отрицательные, например, в неориентированном графе ячейка (1, b) содержит 1, а в орграфе -1. Действительно, это уместно, т. к. в первом случае ребро b не направленное, а во втором – направленное, и, причем вершиной входа для него является вершина «1».
Каждый столбец отвечает за какое-либо одно ребро, поэтому граф, описанный при помощи матрицы инцидентности, всегда будет иметь следующий признак: любой из столбцов матрицы инцидентности содержит две единицы, либо 1 и -1 когда это ориентированное ребро, все остальное в нем – нули.
В программе матрица инцидентности задается, также как и матрица смежности, а именно при помощи двумерного массива. Его элементы могут быть инициализированы при объявлении, либо по мере выполнения программы.